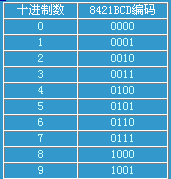
8421BCD码　　

二进制编码的十进制数，简称BCD码(Binarycoded Decimal). 这种方法是用4位二进制码的组合代表十进制数的0，1，2，3，4，5，6 ，7，8，9 十个数符。4位二进制数码有16种组合，原则上可任选其中的10种作为代码，分别代表十进制中的0，1，2，3，4，5，6，7，8，9 这十个数符。最常用的BCD码称为8421BCD码，8.4.2.1 分别是4位二进数的位取值。 右图为十进制数和8421BCD编码的对应关系表：

　　1、BCD码与十进制数的转换

　　BCD码与十进制数的转换.关系直观，相互转换也很简单，将十进制数75.4转换为BCD码如:
　　75.4=(0111 (0101.0100)BCD 若将BCD码1000 0101.0101转换为十进制数如: (1000 0101.0101)BCD＝85.5
　　注意:同一个8位二进制代码表示的数，当认为它表示的是二进制数和认为它表示的是二进制编码的十进制数时，数值是不相同的。
　　例如：00011000，当把它视为二进制数时，其值为24；但作为2位BCD码时， 其值为18。
　　又例如00011100，如将其视为二进制数，其值为28，但不能当成BCD码，因为在8421BCD码中，它是个非法编码 .
　　2、BCD码的格式

　　计算机中的BCD码，经常使用的有两种格式，即分离BCD码，组合BCD码。
　　所谓分离BCD码，即用一个字节的低四位编码表示十进制数的一位，例如数82的存放格式为：
　　_ _ _1 0 0 0 _ _ _ _0 0 1 0 其中_表示无关值。
　　组合BCD码，是将两位十进制数，存放在一个字节中，例82的存放格式是1000 0010
　　3、BCD码的加减运算
　　由于编码是将每个十进制数用一组4位二进制数来表示，因此，若将这种BCD码直接交计算机去运算，由于
　　计算机总是把数当作二进制数来运算，所以结果可能会出错。例：用BCD码求38+49。
　　解决的办法是对二进制加法运算的结果采用"加6修正,这种修正称为BCD调整。即将二进制加法运算的结果修正为BCD码加法运算的结果,两个两位BCD数相加时,对二进制加法运算结果采用修正规则进行修正。修正规则：
　　(1)如果任何两个对应位BCD数相加的结果向高一位无进位，若得到的结果小于或等于9,则该不需修正;若得到的结果大于9且小于16时,该位进行加6修正。
　　(2)如果任何两个对应位BCD数相加的结果向高一位有进位时(即结果大于或等于16),该位进行加6修正.
　　(3)低位修正结果使高位大于9时,高位进行加6修正。
　　下面通过例题验证上述规则的正确性。
　　用BCD码求35+21 BCD码求25+37 用BCD码求38+49 用BCD码求42+95
　　用BCD码求91+83 用BCD码求94+7 用BCD码求76+45

　　两个组合BCD码进行减法运算时,当低位向高位有借位时,由于"借一作十六"与"借一作十"的差别,将比正确的结果多6,所以有借位时,可采用"减6修正法"来修正.两个BCD码进行加减时,先按二进制加减指令进行运算,再对结果用BCD调整指令进行调整,就可得到正确的十进制运算结果。 实际上，计算机中既有组合BCD数的调整指令，也有分离BCD数的调整指令。另外,BCD码的加减运算,也可以在运算前由程序先变换成二进制数,然后由计算机对二进制数运算处理,运算以后再将二进制数结果由程序转换为BCD码。

  

• 评论内容...
• 匿名发表
• [添加到收藏夹]
• 发表评论：(匿名发表无需登录，已登录用户可直接发表。) 登录状态：未登录