随着科技的发展,对信号发生器各方面的要求越来越高。传统的信号发生器由于波形精度低、频率稳定性差等缺点,已经不能满足许多实际应用的需要,所以必须研究新的信号发生器以满足实际应用的要求。近年来,直接数字频率合成器(DDS)由于其具有频率分辨率高、频率变换速度快、相位可连续变化等特点,在数字通信系统中已被广泛采用。随着微电子技术的发展,现场可编程门阵列( FPGA)器件得到了飞速发展。由于该器件具有速度快、集成度高和现场可编程的优点,因而在数字处理中得到广泛应用,越来越得到硬件电路设计工程师的青睐。
1 DDS的基本原理
DDS的主要思想是从相位的概念出发合成所需的波形,其结构由相位累加器,相位—幅值转换器, D/A转换器和低通滤波器组成,是Tierney, Rader和Gold于1971年提出。它的基本原理框图如图1所示。

图1 DDS的原理框图
图1中, fc 为时钟频率, K为频率控制字, N 为相位累加器的字长, m 为ROM地址线位数, n为ROM的数据线宽度(一般也为D/A转换器的位数) , fo 为输出频率, 输出频率fo 由fC 和K共同决定: fo = fC×K/2N 。又因为DDS遵循奈奎斯特(Nyquist)取样定律:即最高的输出频率是时钟频率的一半,即fo = fC/2。实际中DDS的最高输出频率由允许输出的杂散水平决定,一般取值为fo ≤40% fC。
对DDS进行优化设计,目的是在保持DDS原有优点的基础上,尽量减少硬件复杂性,降低芯片面积和功耗,提高芯片速度等。
2 优化构想
为了减小DDS的设计成本, 对其结构进行优化,优化后DDS的核心结构框图如下所示。
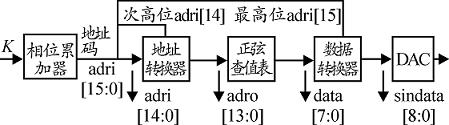
图2 优化后的DDS核心框图
其中的地址转换器是根据adri[14]的数值判断数值是增长(0~π/2)或减少(π/2~π) ,数据转换器是根据adri[15]的数值判断生成波形的前半个周期(0~π)或者后半个周期(π~2π) 。
2. 1 流水线结构
将32位累加器分成4条流水线,每条流水线完成8位的加法运算,流水线的进位进行级联, 运用流水线结构可以提高累加器的运算速度3倍多。为了提高运算速度,加法器采用的是目前速度最快的预先进位算法;为了避免因预先进位传输链过长而影响速度,每8位加法器由两个4位加法器实现。如图3所示:
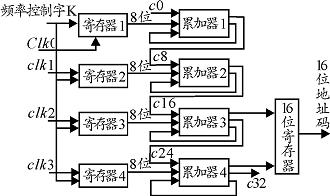
采用流水线结构可以提高器件的运算速度。但是缺点是数据需要保持4个时钟周期,降低了系统跳频的跳变频率。
2. 2 加法器最低位的修正
提取相位累加器的高16位输出作为ROM的查找地址,输出截位减少了ROM的容量,损失的低16位对生成波精度造成的误差可以忽略不计;但因此产生的截位误差却会对频谱纯度和输出带宽产生影响。实验表明当频率控制字K和截位误差2(32-16) 在为互质数的情况下可以将影响减到最小。解决的办法是在相位累加器的最低位加入c0,相位累加器的字长变为32 +1位,截位误差为2(32-16)+1 ,即频率控制字(奇数)和截位误差(偶数)之间互质。这样带来地址上1/2LSB的误差影响,但是在实际应用中可以忽略。
2. 3 ROM的压缩:三角近似法
三角近似法是利用三角恒等式近似的方法对ROM容量进行压缩:因为sin(A+B+C) = sin(A+B)cosC + cosAcosBsinC + sinAsinBsinC,当A 远大于B 和C时,则利用三角近似cosB≈1, sinC≈0 ,上式可以简化为: sin(A+B+C) = sin(A+B) + cosAsinC 。这样可以将ROM转化为两个较小的ROM,分别存储sin (A+B)和cosAsinC的值,这两个ROM的总容量为2A(2B+2C) 。从频谱和ROM容量两方面进行考虑,对于14位地址的最佳分割是: A=5,B=4,C=5。
对ROM表的压缩,是利用相位累加器的次高位来判断象限,将正弦合成波合成到0~π范围;最高位作为符号位, 将正弦波合成到0~2π范围。对于余弦波,符号位是由最高位与次高位异或得到,因为余弦波形比正弦波形提前π/2相位。但是因为正弦函数和余弦函数关于π/4对称,因此可以只存储(0~π/4)的正弦和余弦函数值,这样存储器大小将减小一半。相位累加器的次次高位可以在0~π/4和π/4~π/2之间选择。实际电路实现时,次次高位是与次高位异或产生这个信号。另外,为了完成正交输出,还要增加两个2:1多路选择器电路。
3 DDS的Verilog HDL实现
Verilog HDL语言专门面向硬件与系统设计,可以在芯片算法、功能模块、结构层次、测试向量等方面进行描述,是当前ASIC设计的主要语言之一。
3. 1 四位超前进位加法器的主要源程序:
g[i] = a[i]&b[i]; p[i] = a[i] | b[i];
always@ ( a or b or gnd or g or p )
begin
carrychain[0] = g[0] | p[0]&cin;
sum[0] = p[0] ^cin;
for (j= 41;j<4;j=j+4b1)
begin
carrychain[j] = g[j] | p[j]&carrychain[j-1];
sum[j] = p[j] ^carrychain[j-1];
end
cout = carrychain[3];
end
3. 2 流水线加法器阵列及最低位修正的实现
claadd8s U_add1 (pipe1, SYNCFREQ[7:0], gnd,add1,c1);
claadd8s U_add2 (pipe2, SYNCFREQ[15:8],pipec1,add2,c2);
claadd8s U_add3 (pipe3, SYNCFREQ[23:16],pipec2,add3,c3);
claadd8s U_add4 (pipe4, SYNCFREQ[31:24],pipec3,add4,c4);
在此调用了8 位超前进位加法器,用VerilogHDL 的结构描述方法实现,对应于用电路图输入逻辑。四个加法器在不同的时钟控制下工作,实现流水线结构; pipe1、pipe2、pipe3、pipe4分别为各自加法器的和; SYNCFREQ 是32 位频率控制字, gnd、pipec1、pipec2、pipec3是加法器的输入进位位, c1、c2、c3、c4是加法器的输出进位位。
3. 3 波形折叠和抬高算法
3.3.1 波形折叠(地址转换器)
always@ (adri)
if (adri[14] )
adro = 14h1ff^adri[13:0];
else
adro = adri;
end
endmodule
3.3.2 抬高算法(数据转换器)
always@ ( data or adri[15] ) begin
if (!adri[15] ) sindata = 9h1ff^data;
else sindata= data - 9h001;
end
result = {!adri[15] , sindata};
end
根据adri[14]的数值判断地址码是否需对π/2进行折叠。用^(按位异或) 实现对地址码对π/2 的折叠:用全1减去adri的数值,因为被减数是确定的而且是全1,所以用异或实现减法,比用减法器节省门数。
根据adri[15]的数值判断波形的正负:若是正,则用全1和从ROM中取出的值相加,相当于原数据减1后再在最高位拼接1,以1LSB 的偏移量为代价,省略减法器;若是负,则用按位异或实现减法,得到经过抬高处理的数据。抬高处理是为了使DAC的输入全为正数。
3. 4 压缩sin值ROM查值表
rom1 U_rom1 (QWAVESIN , MODPHASE , SYSCLK , RESETN) ;
rom2 U_rom2 (product , QWAVESIN2 , QWAVESIN1 , SYSCLK , RESETN) ;
其中rom1 是sin(A+B) 值的存储表rom2 是cosAsinC值的存储表。QWAVESIN是rom1表的输出,MODEPHASE是从累加器输出的量化正弦值。p roduct是rom2 的输出, QWAVESIN2 , QWAVESIN1 分别是cosA和sinC 的值。再由9 位加法器将rom1 和rom2的输出相加,就可得到正弦查值表的完整输出。在MAX + PLUSII下的正弦查值表的输出如下图所示。
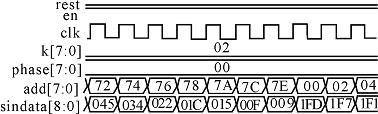
实验表明,所设计的DDS在满足性能的条件下,提高了芯片工作速度,节约了芯片面积,改善了频谱性能。
4 结束语
本文给出了利用Altera 公司的FLEX10K设计DDS的方法,并得到了一些改进:使用流水线算法和输入寄存器可以在不过多增加门数的条件下,大幅度提高芯片的工作速度;修正加法器最低位带来3dB左右的频谱性能提高,提高了输出波形的频谱纯度;压缩ROM的容量,可以使芯片在满足性能的基础上节约了芯片资源。



 Alexa
Alexa mcusy_cn#126.com (请把#改成@)
mcusy_cn#126.com (请把#改成@)  交流:522422171
交流:522422171 51/AVR单片机技术驿站! <
51/AVR单片机技术驿站! <









 最新评论
最新评论