| 计数器 |
计数器的分类:
按进位模数分为模2计数器和非模2计数器。
进位模是计数器所经历的独立状态的总数,也就是进位制数。
模2计数器就是进位模为2n的计数器。其中n为触发器的级数;非模2计数器就是进位模非2n的计数器。
按计数脉冲的输入方式分为同步计数器和异步计数器。
同步计数器是相应的触发器的计数脉冲也相同,使相应的触发器同时翻转。异步计数器是相应的触发器的计数脉冲不相同,并且不同时翻转。
按计数增减趋势分为递增计数器、递减计数器和双向计数器。
递增计数器是每来一个时钟脉冲触发器的组成状态按二进制代码规律增加,递减计数器就是按二进制代码规律减少。双向计数器是可增可减,由控制端来决定。
按电路集成度分为小规模集成计数器和中规模集成计数器。 |
| 1、同步计数器的分析与设计 |
| 在设计同步计数器是由于已经明确了状态数、状态代码和状态迁移关系,所以不需要制作原始状态图、状态化简和状态分配。 |
|
1、二进制计数器的设计
模为2的同步计数器称为二进制计数器,它的特点是没有多余状态,触发器的利用率高。它通常是采用自然二进制编码。 |
|
例1.设计一个三位二进制同步递增计数器.
三位二进制的进位模数为23=8,它的状态表为:如图(1)所示.状态迁移图为:如图(2)所示 |
|
|
|
|
|
将现态QCn、QBn、QAn作为输入,次态QCn+1、QBn+1、QAn+1作为输出,通过卡诺图可得出各触发器的次态方程为: |
|
QCn+1=QAnQBnQCn+QAnQCn+QBnQCn=QAnQBnQC+QAnQBnQC
QBn+1=QAnQBn+QAnQBn
QAn+1=QAn
把求得的次态方程与选用触发器的特征方程作比较,求得各触发器的激励函为: |
|
Jc=QAnQBn
JB=QAn
JA=1 |
Kc=QAnQBn
KB=QAn
KA=1 |
|
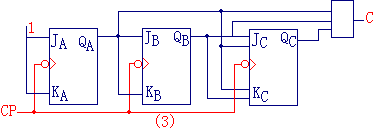
它的逻辑电路图为: |
如图(3)所示 | |
|
|
位数增多的二进制计数器的设计可按以上方法进行,当位数>5时,就不能用上面的方法了(卡诺图不易制),从上面的例子我们可以看出:低级触发器除外,每一位触发器的J,K激励函数都是由它的低位各触发器原码相与而成.由此就可以设计更多位的二进制计数器了.
二进制的减法计数器的设计方法与加法相似,只不过状态迁移图不同. |
|
2.非2n进制计数器
由于这种进制不是2的倍数,所以存在着多余状态,在设计中应把这些多余状态作无关项来考虑.在实际中用的最多的是十进制计数器,它需要四个触发器. |
| 例1.五级触发器的进位模数最大为:( ) |
| A.五进制 |
B.十进制 |
C.十六进制 |
D.三十二进制 |
| 因为是五级触发器,所以它的最大进位模数为25=32,所以答案为 D |
|
例2.设计一个模六计数器.
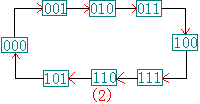
由于22<6<23,所以模六计数器需要三级触法器组成.三级触法器有8种状态,因此存在着两种多余状态,我们任选其中的六种,它的状态图为:如图(1)所示, |
|
我们通过各级触发器(用JK触发器来实现)的卡诺图可得各级触发器的次态方程为:
QCn+1=QAnQCn+QAnQCn
QBn+1=QBnQCn+QBnQCn
QAn+1=QAnQBn+QAnQBn
C=QAnQBn
由次态方程可得激励方程为: |

| |
|
Jc=QAn
JB=QCn
JA=QBn |
Kc=QAn
KB=QCn
KA=QBn |
|
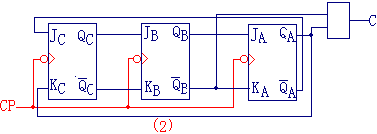
| 所的逻辑电路图为:如图(2)所示 | |
|
这类计数器由于状态没有用完,存在着多余状态,所以它就有一个自启动和自校正问题.
自启动就是当电源合上之后,电路能否进入所用的状态之中的任一状态,如果能则有,否则即无.
自校正就是计数器正常工作时,由于一些原因,使计数状态离开正常的的序列,若经过若干个节拍后电路如能返回正常的计数序列,则有校正能力.如不能,则无校正能力.
注: 具有自校正能力的计数器也具有自启动能力.
怎样判断电路是否具有自校正能力呢?
一般是把未用的状态代入所得的次态方程,求得次态,并判断次态是否还是无用状态,若是则表示无自校正能力,若转入有用序列则表示该电路具有自校正能力。 |
|
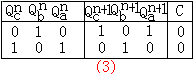
根据上面的结论,来判断一下例2是否具有自校正能力。先把没用的两种状态代入次态方程,结果为:如图(3)所示由此可以看出此电路无自校正能力,因此要改进设计。 |
|
改进的具体步骤是:
切断010与101的无效循环序列,强迫使之进入110,由于前两级都没有改变,所以只需重新设计第三级即可. |
| |
|
QCn+1=QAnQCn+QAnQBnQCn
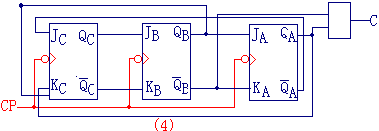
则改进后的逻辑电路图为:如图(4)所示 |
|
|
| 3.同步时序电路的分析 |
| 它的分析方法和步骤与同步时序电路是一样的.在这里我们就不多说了. | |



 Alexa
Alexa mcusy_cn#126.com (请把#改成@)
mcusy_cn#126.com (请把#改成@)  交流:522422171
交流:522422171 51/AVR单片机技术驿站! <
51/AVR单片机技术驿站! <









 最新评论
最新评论