|
1、组合电路竞争冒险的现象
前面在对组合逻辑电路进行分析及设计时,皆在针对器件处于稳定的工作状态的,而没有考虑器件的信号变化的瞬间的情况,为了保证电路工作的稳定性及可靠性,必须对其输入的变化的情况下输出的稳定性。
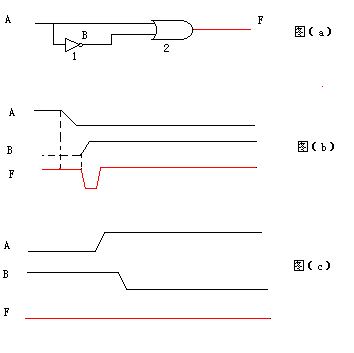
上图a为一个非门与或门构成的电路,当输入信号A由1变为0时,则或门2的两个输入信号,一个由1变为0,一个由0变为1,电路稳定时其输出F=1,按照电路逻辑函数式,输出F应恒为1。但是,信号在状态转换过程中,由于存在着上升和下降时间,每个门电路又有传输延迟时间,因此实际F信号出现了负向脉冲,见图(b)所示。这是因为B是由A经反相器1延迟后到达门2,所以B的变化落后于A的变化。当A已下降为低电平时,B还处于低电平状态,经或门2传输延迟后,F出现了负向过渡干扰脉冲。通常,把门2这两个互补信号同时向相反方向变化的现象叫竞争。
可是,存在竞争现象的电路不一定都产生过渡干扰脉冲。例如,上例中当信号由0变为1时,虽然门2也有向相反状态变化的两个输入信号,但因A先由0变为1,B后由1变为0,他们不存在同时为0的情况,故F恒为1,不会产生干扰脉冲,见图(C),可见,电路中有竞争现象只是存在产生过渡干扰脉冲的危险而已,故称其为竞争冒险。
上图b给出了其输入与输出的波形,其中红色的波形为输出波形,从图上可以看出,其输出不是固定为1,而是有一段时间内其为0,这是什么原因造成的呢?
我们在前面设计和分析电路时,没有考虑器件的延时问题,而实际的器件是存在延时的,竟争冒险现象就是由于器件的延时造成的,没有延时的话其将没有竟争冒险。
上图中是在或与输入端的两个输入的变量正好相反,其实在与输入端的两个变量正好相反并且有延时的话同样会出现竟争冒险的现象。
2、组合电路竞争冒险的判断
★代数法
判断有没有竟争冒险现象,只要判断任意一个与输入、或输入的变量是会不会出现两个输入变量相反、或两个输入相同但经过的路径不同,如果满足上面的情况,则可能存在竟争冒险的现象,这可以很方便用代数法加以判断。
★卡诺图法
除上面的判断方法还可以用卡诺图进行判断,下图为前面卡诺图化简的一个例子,在这两种圈法中很显然其第二种更简单,第一种不是最简,但在竟争冒险的判断中,第一种不存在,而第二种却存在竟争冒险现象。利用卡诺图法进行判断的规则:观察卡诺图中的是否有两个圈相切但不相交,如有则存在竟争冒险现象,很显然其第二图是只相切但不相交,而第一个图是全部相交的,故其没有竟争冒险现象。
3、组合电路竞争冒险的消除
为了说明消除竞争冒险的方法,我们来分析下面的组合电路
由该电路逻辑图可直接写出输出函数式:
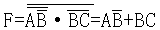
假定A=C=1时,该电路的逻辑关系和上图(a)基本相同。函数可以写作:
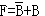
当B由1变为0时,由于信号传输路径不同,F先由0变为1,E后由1变为0,使F和E出现同时为1的时刻,故输出产生负向过渡干扰脉冲。因此,该电路存在竞争冒险现象。
如何消除竞争冒险现象呢?下面介绍两种方法:
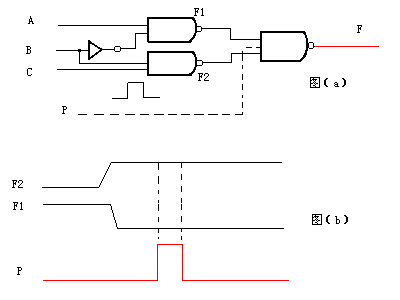
1.加选通脉冲 如上图(a)所示。
该选通脉冲通常是P=0,使电路处于封锁状态,只有在接收了输入信号并且电路达到了新的稳态之后,才有脉冲P=1,允许电路输出。这就避免了竞争冒险的影响。引入选通脉冲的组合电路,输出信号只有在选通脉冲P=1其间才有效,波形图见上图(b)所示。
2.修改逻辑设计
适当修改逻辑电路,可以消除某些竞争冒险现象。例如,上面分析的电路中,当A=C=1时,由于 出现了互补的变化信号,所以存在竞争冒险现象。为此,我们可把表达式变换一下,根据常用布尔公式可知: 出现了互补的变化信号,所以存在竞争冒险现象。为此,我们可把表达式变换一下,根据常用布尔公式可知:
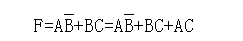
上式增加了AC项以后,函数关系不变,但当A=C=1时,输出F恒为1,不再产生干扰脉冲。所以,把电路按上式修改,即可消除竞争冒险现象。修改后的电路如下图所示:
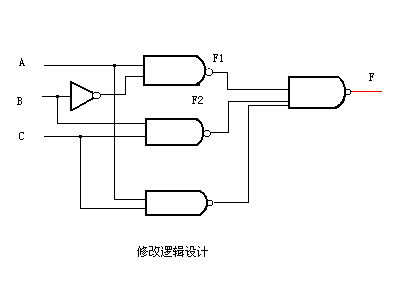
用增加多余项的方法修改逻辑设计,可以消除一些竞争冒险现象,但是,这种方法的适用范围是有限的。不过,只有通过逻辑设计,使得在转换信号时,电路中各个门的输入端只有一个变量改变状态,则输出就不会出现过渡脉冲干扰,从而消除了竞争冒险现象。
★冗余项法
增加多余项的方法修改逻辑设计,可以消除一些竞争冒险现象,但是,这种方法的适用范围是有限的。
★选通法
我们可以在电路上加上一个选通信号,当输入信号变化时,输出端与电路断开,当输入稳定后,选通信号工作,使电路输出到输出端。
★滤波法
从实际的竟争冒险的波形上可以看出,其输出的波形宽度非常窄,我们可以在输入端加上一个小电容来滤去其尖脉冲。 | 


 Alexa
Alexa mcusy_cn#126.com (请把#改成@)
mcusy_cn#126.com (请把#改成@)  交流:522422171
交流:522422171 51/AVR单片机技术驿站! <
51/AVR单片机技术驿站! <






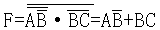
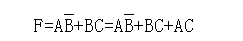

 最新评论
最新评论